這篇筆記因為是上課筆記,所以會先記上課的為主。
但因為課程講的東西有點雜,所以後面會以用書為主,今天先寫對於灰階的cnn,下一篇會開始寫對於彩色的圖片怎麼做,其應用又該怎麼做。
CNN 圖片如下,可以先看看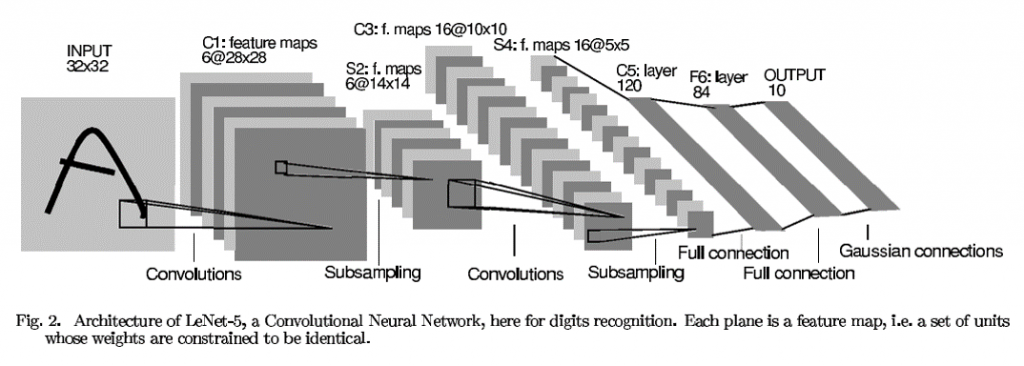
課程是從44分才開始講CNN
從課程開始我們就有用到CNN,這節課是在跟我們說他的原理
CNN的C 就是卷積的意思,
卷積的概念網路上很多
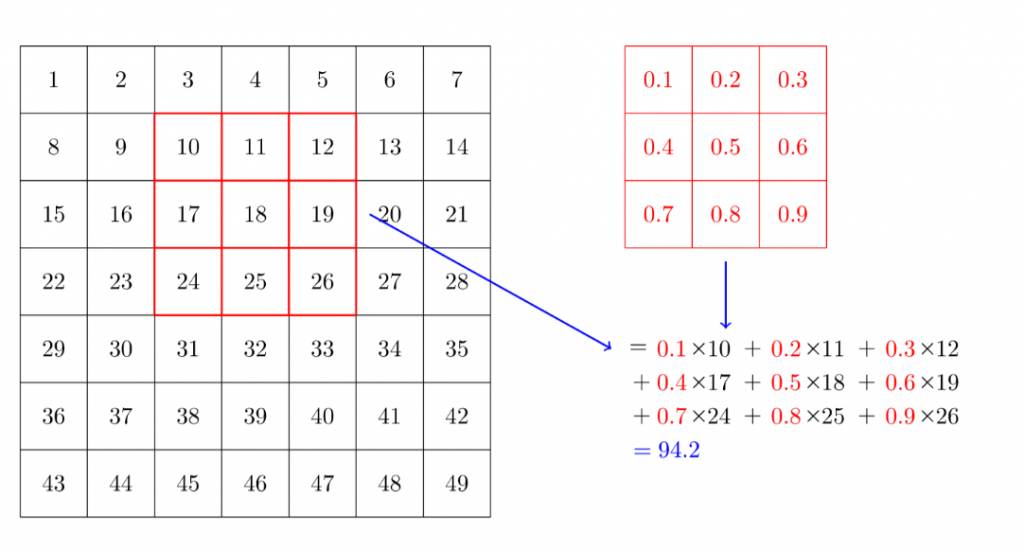
基本上就是定義一個n*n 的矩陣,讓這個矩陣掃過圖片的像素,都對這個矩陣做運算
而得到一個新的矩陣,這個新矩陣我們叫做feature map,所以不同的kernel會得到不同的feature map。
所以CNN可以讓我們不再是人工找特徵,而是讓神經網路來幫我們找了
這意思是什麼呢? 如我們學習的影像處理,我們需要定義kernel ,才能得到不同的特徵
然後根據這些人工算出的特徵,再由機器學習幫我們定義權重
但問題就出現在這邊,如果你沒有定義到幾個真正有用的kernel,那機器學習能幫忙的也很有限
意思就是你沒有給足夠有用的特徵。
而這部份,神經網路可以幫我們設計kernel ,
而神經網路就可以用這些卷積出來的矩陣,透過sgd 等等的方式(之後會說),來做出一個新模型
那以下來看看這個kernel 是怎麼幫我們算出feature map的
所以知道CNN的基本原理後,我們就介紹一些不同的優化方法,可以加進去設計的。
什麼是池化層?,他對我們的幫助是什麼呢?
其實這也算是kernel 的一種,但是他可以幫我們有效減少計算量又不損失太多圖形細節
什麼意思呢?
就像你看高解晰圖片可以辨識那是什麼東西
給你馬賽克圖片 你可能也辨識得出來是什麼??
用馬賽克當例子有點誇張,但意思就是損失一些訊息,我們還是可以得到我們想要的結果
而這樣卻可以大幅度的減少計算量。
同時因為這樣還有其他好處,就是說因為我們可能經過一些平均,而讓整個圖型在訓練的時候就已經是糊糊的,這樣就不會因為太精細的一些特徵,而失去robust的特性,也可以避免太多特徵,而降低overfitting的機會
那要怎麼做呢? 我們來看看
而池化層這種如果一直縮小featuremap , 到最後就會失去表述力,所以通常會在後面加一層desnse layer(全連接層)
同樣的卷積也可以做到這種縮小,也就稱為Strided Convolution:例如使用用Stride 2,每滑一次就跳過中間的一層

如果設定stride =2 跳過中間的,就像這樣
那到底要用max pool 還是要用average pool ,這也是我們需要調整的地方
這個設計,講師說fastai 有設計幫我們主動去嘗試這2種,我們之後應該會學到。
後面看了一下講師只是提了很多不同的經驗,但是對於初學者的我們其實很難抓到他想說的。
所以我想還是看他的書,從頭來看cnn。
所以這邊用了書中的13章notebook 來學習cnn
那我們要用到的資料集是什麼呢?
是手寫識別資料集 MINST
先來看其中一張圖片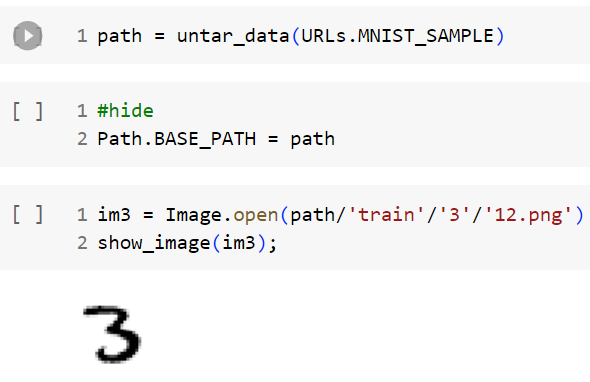
上面說的kernel 計算方法,我們用pytorch 幫我們跑跑看
先定義一個kernel
top_edge = tensor([[-1,-1,-1],
[ 0, 0, 0],
[ 1, 1, 1]]).float()
然後我們取這張3的最左上方3x3 的大小來跟這個kernel 做相乘,最後加總
好,結果是0,但左上本來就是白白的所以沒什麼感覺
下面挑了3的頂部邊界來卷卷看,至少會有值。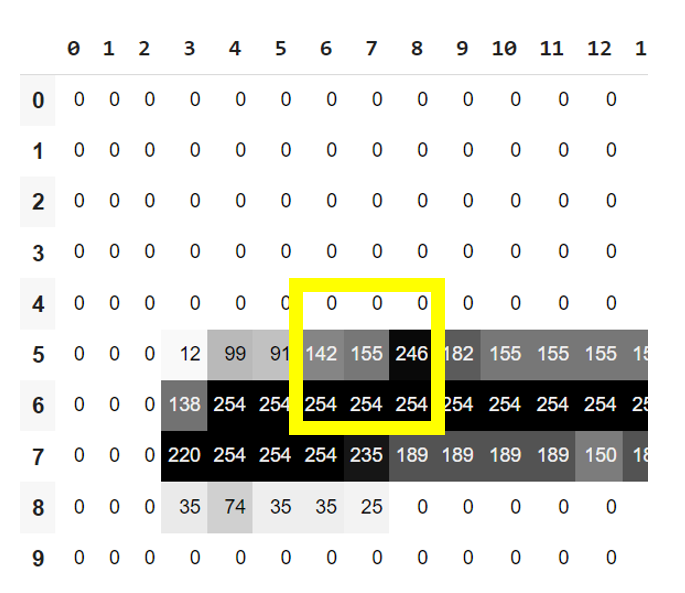
(im3_t[4:7,6:9] * top_edge).sum()
#output is tensor(762.)
再挑右下角的邊界來卷卷看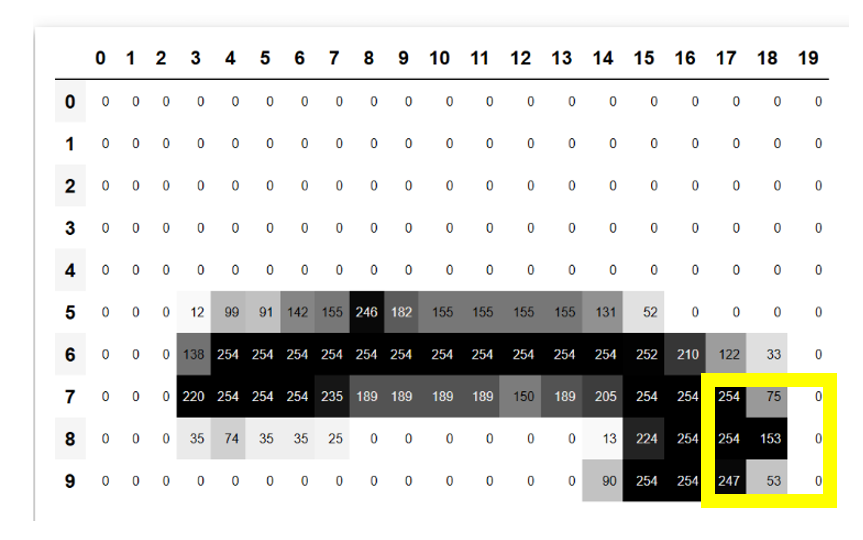
(im3_t[7:10,17:20] * top_edge).sum()
# output is tensor(-29.)
藉由頂部與底部的計算,我們可以看到kernel 的-1 跟1 的影響
所以這樣可以分析出水平的邊緣
注意到我們的kernel 這時定義的是 最上面是3個-1,最下面是3個1
也就是說,如果我們的kernel 掃過去時,最上面的3格會跟底部的3格相減,
相減就是看誰大吧,如果底下的大,那就會是正,如果底下的小,就會是負數
對於每一格來說,數字越大,就表示顏色越深,所以如果總和是正數,就代表底下的顏色比上面深。
下面就定義了一個這個kernel 的運算函式
def apply_kernel(row, col, kernel):
return (im3_t[row-1:row+2,col-1:col+2] * kernel).sum()
但如果這個輸入跑到角點會出錯(這邊沒有針對角點做判斷)
這邊只是做演示,讓我們可以用code來理解卷積
下圖是我們假設有一張5x5 的圖,然後用3x3 的kernel 來做處理。

底下演示了把3 拿來做完卷積的效果,可以看到他的底邊變白,上半部變黑

同樣也可以用不同的卷積,做到左邊的邊界加強

這些就是卷積對於圖形操作的效果,所以應用不同的kernel ,卷出來的效果也不同,也就是說,對於一張圖片他可以有不同的解釋,但這些解釋我們要他歸納出一個結論:這是3。
這些動作,如前面所述,我們不想主動設計,希望神經網路來幫我們做。
那要做到這件事的話,我們先來時看看pytorch 可以幫到我們什麼。
fastai 有定義了一個F類別是從from torch.nn.functional來的,其中定義了F.conv2d
那該如何使用呢? 先來看他的參數什麼。
input 是一個形狀為 (minibatch, in_channels, iH, iW) 的張量,其中:
minibatch 表示一批(batch)數據中的樣本數量。
weight 是一個形狀為 (out_channels, in_channels, kH, kW) 的張量,其中:
在此例中 ,圖形的寬高是(iH,iW)=(28,28),kernel的寬高則是(kH,kW)=(3,3)
這邊書上說pytorch期望讓這2個參數收到rank-4 張量,但目前我們只有rank-2 張量,老實說看不懂
查了一下如下所示:
單個圖像的 rank-4 張量:
如果我們考慮一個彩色圖像,該圖像的形狀為 (3, 32, 32),這意味著有 3 個通道(紅色、綠色和藍色),每個通道的高度和寬度都是 32 像素。這個圖像可以表示為 rank-4 張量,其中的軸分別對應於批次大小、通道、高度和寬度。
形狀:(1, 3, 32, 32),這是一個 rank-4 張量,其中包含一個圖像。
多個圖像的 rank-4 張量:
當我們處理多個圖像時,通常會將它們一起組成一個批次。假設我們有一個批次包含 64 個彩色圖像,每個圖像的大小和通道數相同。
形狀:(64, 3, 32, 32),這是一個 rank-4 張量,其中包含 64 個圖像。
卷積核的 rank-4 張量:
在卷積神經網絡中,卷積核也可以表示為 rank-4 張量,其中的軸分別對應於輸出通道、輸入通道、高度和寬度。假設我們有 64 個輸出通道的卷積核,每個卷積核的大小為 3x3,並且來自 3 個輸入通道。
形狀:(64, 3, 3, 3),這是一個 rank-4 張量,其中包含 64 個卷積核。
好了這邊我們用到的只有rank-2 張量,上面的要等後面講處理彩色圖的時候再使用。
以下提到pytorch 的2個小技巧。
這邊我想是pytorch 有幫我們用gpu來做這些平行運算,讓我們不用自己處理來達到高效運算。
現在建立2個對角邊kernel ,然後把全部的4個邊角kernel 疊成一個張量。如以下程式:
diag1_edge = tensor([[ 0,-1, 1],
[-1, 1, 0],
[ 1, 0, 0]]).float()
diag2_edge = tensor([[ 1,-1, 0],
[ 0, 1,-1],
[ 0, 0, 1]]).float()
edge_kernels = torch.stack([left_edge, top_edge, diag1_edge, diag2_edge])
edge_kernels.shape
#output is torch.Size([4, 3, 3])
注意這邊的[4,3,3] 只有rank-3,為了輸入到F.conv2d,我們必須補到rank-4 ,最簡單就是補在channel ,數值為1 ,所以這邊可以呼叫一個方法來補,就是unsqueeze(1).shape
正確呼叫方式為
edge_kernels = edge_kernels.unsqueeze(1)
這樣的結果就會是[4,1,3,3]
接下來建立一個dataloader 來試試
mnist = DataBlock((ImageBlock(cls=PILImageBW), CategoryBlock),
get_items=get_image_files,
splitter=GrandparentSplitter(),
get_y=parent_label)
dls = mnist.dataloaders(path)
xb,yb = first(dls.valid)
xb.shape
#output is torch.Size([64, 1, 28, 28])
torch.Size([64, 1, 28, 28])就是說一個批次有64張圖,每一張圖1個通道(灰階),有28x28 的像素。如果是彩色圖形的話,通道就會是3
其中把第1個minibatch 存在xb , yb ,作者這邊接下來要轉成cpu來處理(預設是gpu)
xb,yb = to_cpu(xb),to_cpu(yb)
到這邊就準備好F.conv2d的輸入參數了,讓我們來呼叫看看,並看看他做了第一個卷積後的圖長什麼樣子
batch_features = F.conv2d(xb, edge_kernels)
batch_features.shape
#output is torch.Size([64, 4, 26, 26])
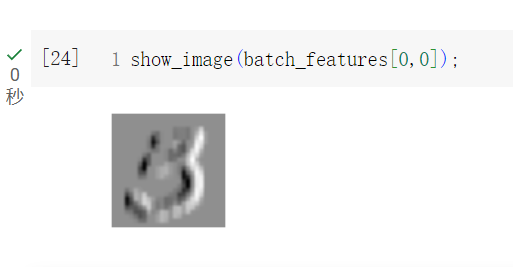
這邊講到課程講的步幅了,一次走幾步再卷,這是一種卷積的小技巧
還有padding ,如同我們做完卷積與池化,也許會讓feature map 變小
,這可能會導致信息的損失。為了保持輸出特徵圖的大小或控制其縮小的幅度,可以使用 padding。Padding 就是在輸入圖像的邊界周圍添加額外的像素值(通常為 0),以擴展輸入的尺寸,從而保持輸出特徵圖的大小。這對於維持空間信息和避免特徵圖縮小太快非常重要,特別是對於深度神經網路,因為它們有多個卷積層。
在某些情況下,padding 也可以有助於處理圖像邊界的特徵,因為輸入圖像邊界的像素通常包含重要信息,這些信息可能在卷積過程中被忽略或損失。

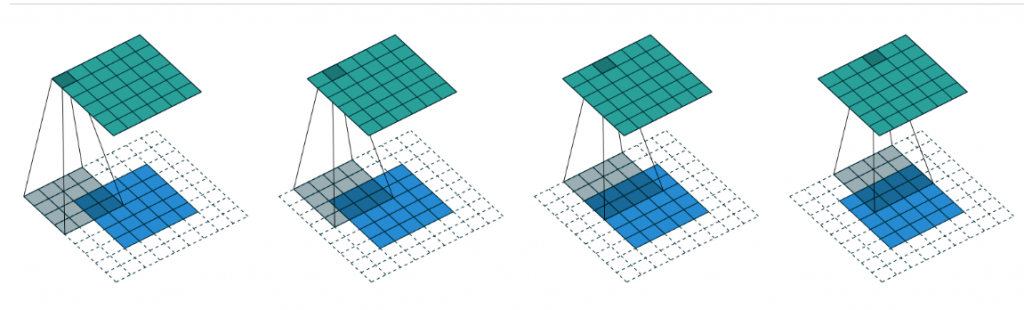
使用步幅的圖 ,最上面有說過,而書上討論到一個重點是,如果是在大小為h*w 的圖中,使用padding 1 與strides2 會產生大小為 (h+1)//2 * (w+1)//2
的結果,而各維的通用公式為:
(n + 2 * pad - ks)//stride + 1
其中
pad=padding
ks 是kernel 大小
看起來很複雜,但這邊只要大概曉得,我們用步幅為2,就會大約縮減一半的feature map
詳細怎麼算先不考慮。
